Дифференциальные уравнения движения Ищите кому заказать термех - присылайте мне вк
Ярким примером этой задачи является семейство задач Д1 – Д3 из сборников задач под редакцией Тарга С.М. и Яблонского А.А. Поэтому советую их скачать и бегло просмотреть. В этих задачах требуется определить какие то величины: закон движения точки на каком либо участке, скорость или какую либо величину – это не важно. Решение задачи сводиться к составлению дифференциального уравнения движения. Как известно – сила это масса умноженная на ускорение. Ну вот тут то же самое, только не сила – а сумма сил действующих на точку. Не ускорение, а вторая производная от перемещения. Далее вводятся координатные оси (если точка движется вдоль наклонной плоскости или по прямой – координатная ось Х пусть будет ей параллельна). Далее находятся проекции на оси координат внешних сил и реакций опор, действующих на материальную точку. Эти проекции приравниваются к массе умноженной на вторую производную соответствующей координаты точки. Если короче – масса точки умноженная на вторую производную от икс по времени равна сумме проекций всех сил, действующих на точку, на эту ось. Если точка движется по прямой, то суммы проекций сил на другие оси равны нулю, так как ускорение движения по этим осям отсутствует (нет движения – нет ускорения). Из таких уравнений обычно находят значение реакции опор для определения модуля силы трения, которая как раз таки будет давать проекцию на ось, вдоль которой совершается движение. Заметим, что направление силы трения противоположно направлению движения материальной точки.
“сила трения равна модулю реакции опор умноженной на коэффициент трения скольжения и направлена в обратную сторону движения”
Помимо силы трения, реакции опор и внешних сил (в том числе и силы тяжести) на тело могут действовать и другие силы: силы сопротивления движению среды, силы упругости, силы притяжения или отталкивания. От того, какие именно или в каком сочетании– зависит вид дифференциального уравнения. Я немного запутал или усложнил суть этого текста, но только для того, чтобы охватить все многообразие существующих дифференциальных уравнения движения материальных точек.
“Сила трения равна произведению коэффициента упругости (жесткости) пружины на ее деформацию. Направлена сила упругости в обратную сторону деформации”
“Сила сопротивления среды движению равна произведению коэффициента вязкости среды (мю) на скорость (или квадрат скорости) движения точки в вязкой среде. Эта сила направлена в противоположную сторону движения”
При решении задач на составление диф. уравнений движения, следует придерживаться следующих рекомендаций: направление координатной оси пусть совпадает с направлением движения. Если есть пружина – пусть она будет на рисунке растянутой, так чтобы проекция силы упругости была отрицательна, пусть начало координат совпадает с положением точки в состоянии статического равновесия (это такое положение, при котором сила упругости, соответствующая статической деформации пружины, уравновешивает силу тяжести, трения и тд). Если есть система пружин – заменим их на пружину с эквивалентной жесткостью (делается как с током в проводах – если две параллельные пружины, то их жесткость складывается, если две последовательно соединенных - то произведение их жесткостей делиться на их сумму). Если имеет место сила притяжения или отталкивания – целесообразно разложить ее на составляющие по осям координат.
Итак, совершенно очевидно, что дифференциальное уравнение движение всегда получается второго порядка. Если значение какой либо силы зависит от времени или в состав диф уравнения входит константа – получается диф. уравнение второго порядка со специальной правой частью. Напомню, что в этом случае решение уравнение будет искаться как сумма общего и частного решений: общим будет решение уравнения с нулем вместо специальной правой части, а частным – с учетом этой правой части. Как видите, после составления диф уравнения, теоретическая механика заканчивается и начинается высшая математика, но не стоит в панике закрывать эту страницу – я постараюсь подробно и просто объяснить что к чему.
“Решение дифференциального уравнения второго порядка со специальной правой частью равно сумме общего и частного решений”
Итак, немного вышки из моей шпаргалки, которую мне написала еще моя преподавательница по высшей математике Боброва Эльвира Ивановна, за что ей большое от нас спасибо. На этой шпоре написан вид общего решения диф. уравнения второго порядка в зависимости от вида корней характеристического уравнения. Ах да, совсем забыл – нужно составить характеристическое уравнение и найти его корни, например:
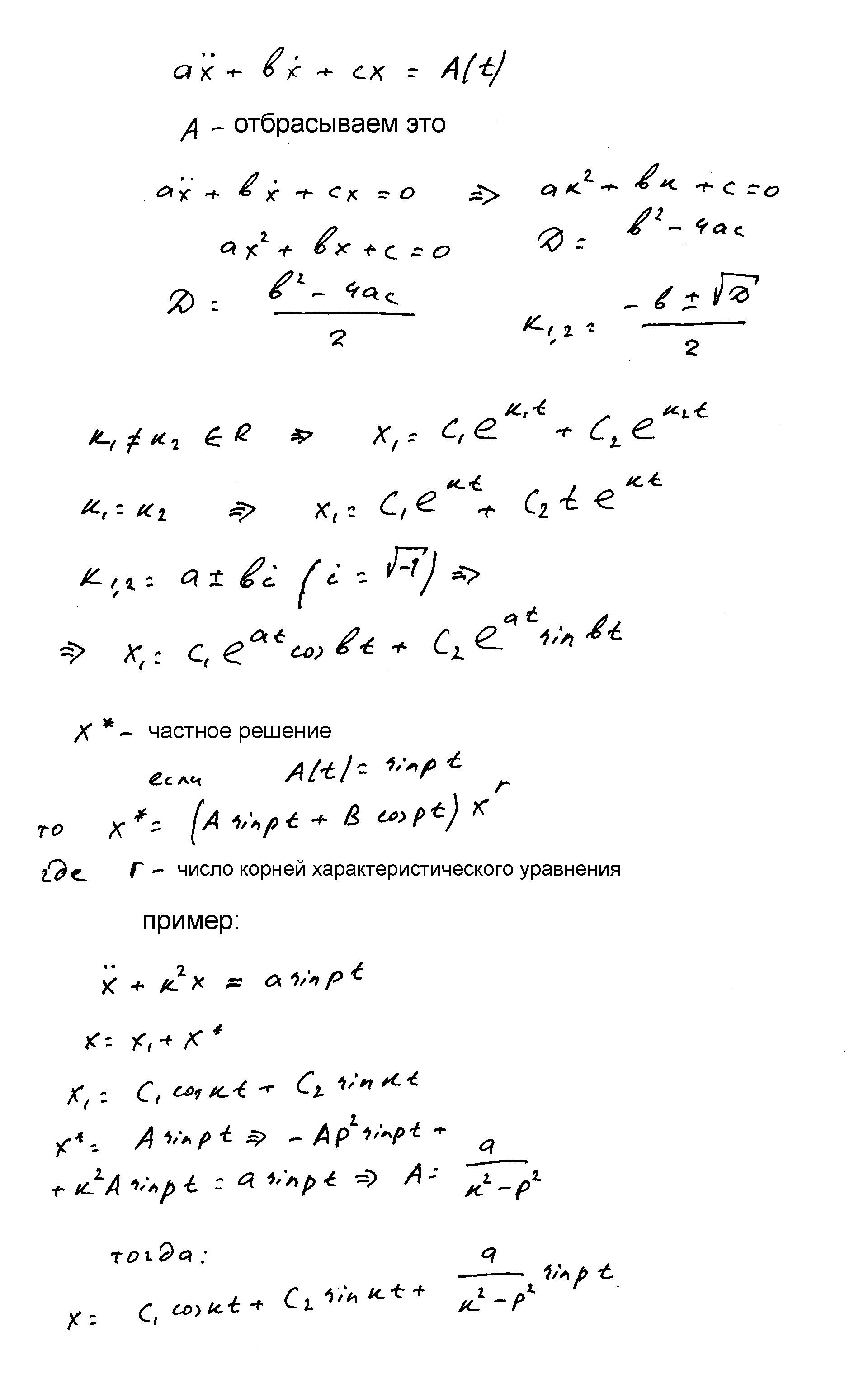 Как видно из шпоры, что бы получить характеристическое уравнения нужно заменить икс с двумя точками на r в квадрате, икс с точкой на r а просто икс вообще убрать. Далее приравниваем к нулю специальную правую часть 9на рисунке я написал что А(t) отбрасываем, где A(t) – и есть спец правая часть. В итоге получается обыкновенное квадратное уравнение, корни которого и являются корнями характеристического уравнения. Находим дискриминант ну и тд. Далее, в зависимости от вида корней характеристического уравнения выбираем в каком виде будем искать общее уравнение диф уравнения (смотри рисунок). Далее бабулька (Эльвира Ивановна те) написала в каком виде искать частное решение, если спец правая часть выглядит вот так A(t) = sinpt , лично я этим не пользуюсь, как то сложно и непонятно для меня. Для решения задач я использую немного другую тактику, можно назвать ее термеховской, или упрощенной. Ниже я написал пример своего решения диф уравнения, из него видно что я ищу частное решение в виде Asinpt , и подставляя его в исходное уравнение определяю значение А, если бы спец часть была косинусоидой (acospt) то я бы искал частное решение как косинусоиду Acospt. Однако без бабулькиной шпоры не понять в каком виде искать общее решение если имеет место не колебание а какое то другое движение, при котором коэффициент при икс отрицателен. Поэтому я бережно хранил все эти годя этот уже сильно поюзаный листок, и вот теперь выкладываю с него бесценные знания). Добавлю – в примере я рассмотрел вынужденное колебание, в котором имеет место возмущающая сила. Ну это из области резонансов, ответов на вопрос почему колонна солдат на мосту не должна идти в ногу и тд.
Итак, пришло время рассмотреть конкретно каждый вид диф.уравнения:
Диф уравнение в котором все величины, кроме икс с двумя точками, постоянные – тупо интегрируется два раза, в полученные уравнения подставляются начальные условия (или какие-нибудь граничные условия, смотря что дано в условии) – это делается для определения констант интегрирования. Далее и полученных уравнений движения (закона движения и закона скорости и ускорения этого движения) находятся искомые величины. Часто это делается подстановкой в уравнения заданных численных данных и значения конечного времени. Бывает по разному, повторюсь – это уже математика, и она явно многоходовая. Если движение происходит на двух участках, то следует составлять диф.уравнения для обоих и совместно их решать. Правило одно – как проинтегрировал диф.ур – подставь в него начальные условия и вместо времени вставь ноль, бывает что даны численные данные для какогото не начального момента времени – тогда подставляем соответствующие цифры и опять таки находим постоянные интегрирования. Таким образом, можно сказать что нахождение констант интегрирования – это предпоследний шаг в решении задачи, а последним будут математические преобрахования полученых уравнений и получения конечного ответа.
Далее рассмотрим гармонические колебания, или проще говоря такие колебания которые не заканчиваються (не затухают) Тут все просто, подставляем в полученные уравнения начальные условия, находим постоянные интегрированя, получаем ответ – закон движения (колебания) точки.
Вынужденные колебанияДалее рассмотрим вынужденные колебания, в этом случае на груз действует возмущающая сила, величина которой изменяется по синусоидальному или косинусоидальному закону. На рисунке я вкратце расписал как искать решение этого уравнения, особо стоит уделить внимание случай резонанса и случая, когда вынужденные и возмущающие движения в противофазе. Главная особенность колебаний при резонансе – амплитуда вынужденных колебаний пропорциональна времени. В этом случае возмущающая сила всегда действует в направлении движения точки (вспоминаем, как выталкивать застрявшую машину в раскачку).
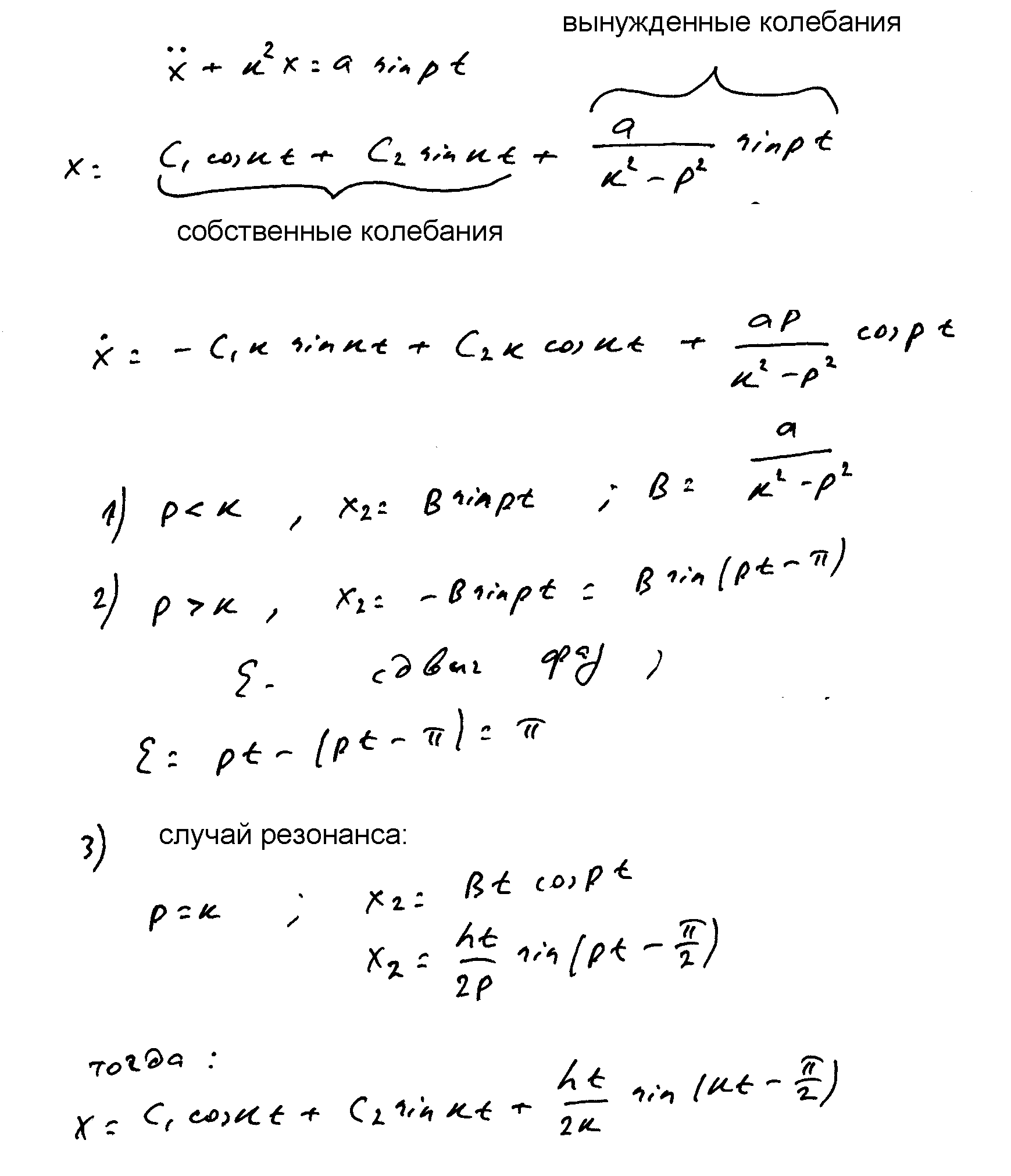 Далее рассмотрим влияние сопротивления на вынужденные колебанияРассмотрим движение точки, когда на нее действует восстанавливающая, возмущающая силы и сила сопротивления:
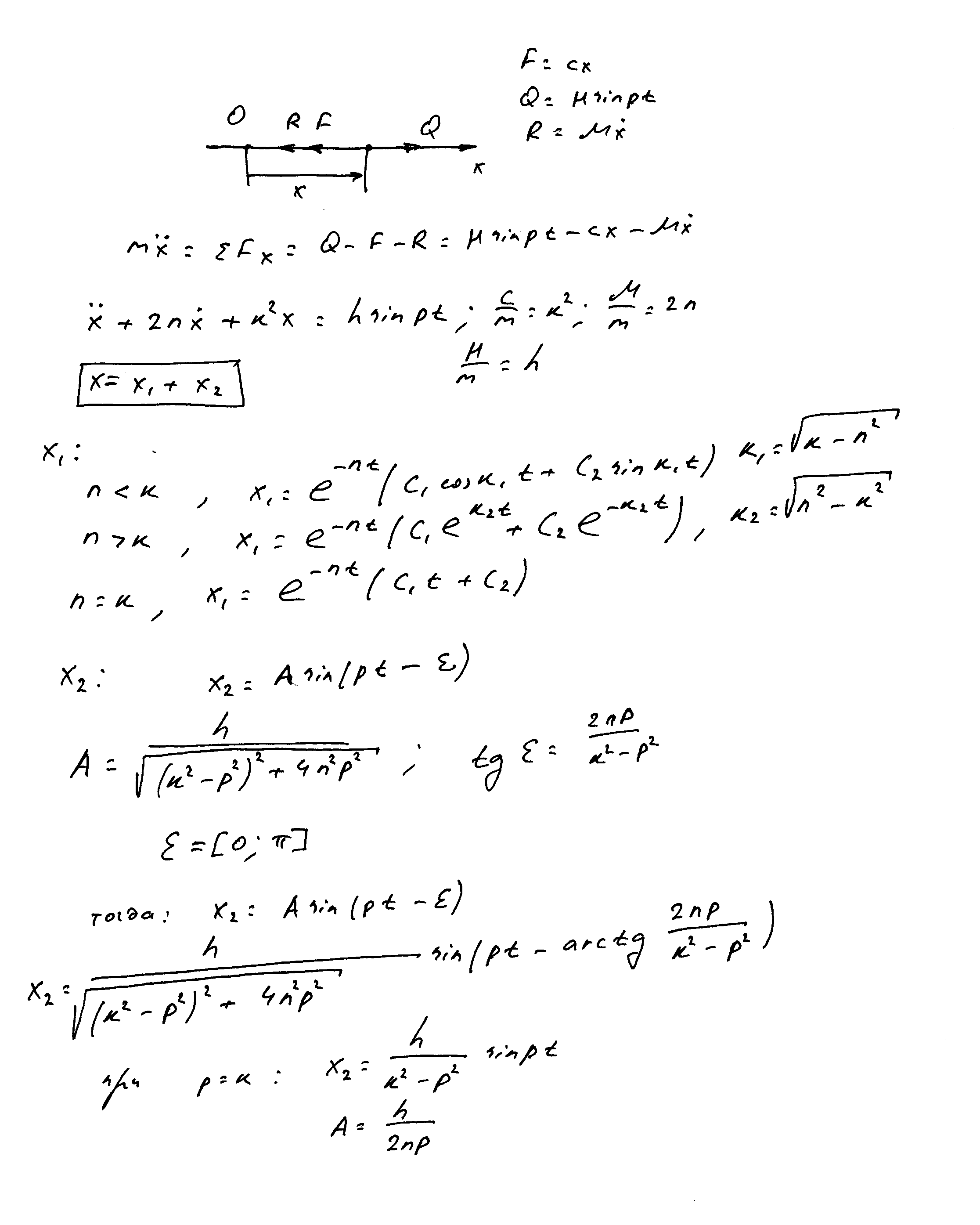 На последок рассмотрим несколько хитростей, которые помогут при решении диф уравнений, вот как можно представить икс с двумя точками (по сути вторую производную перемещения по времени):
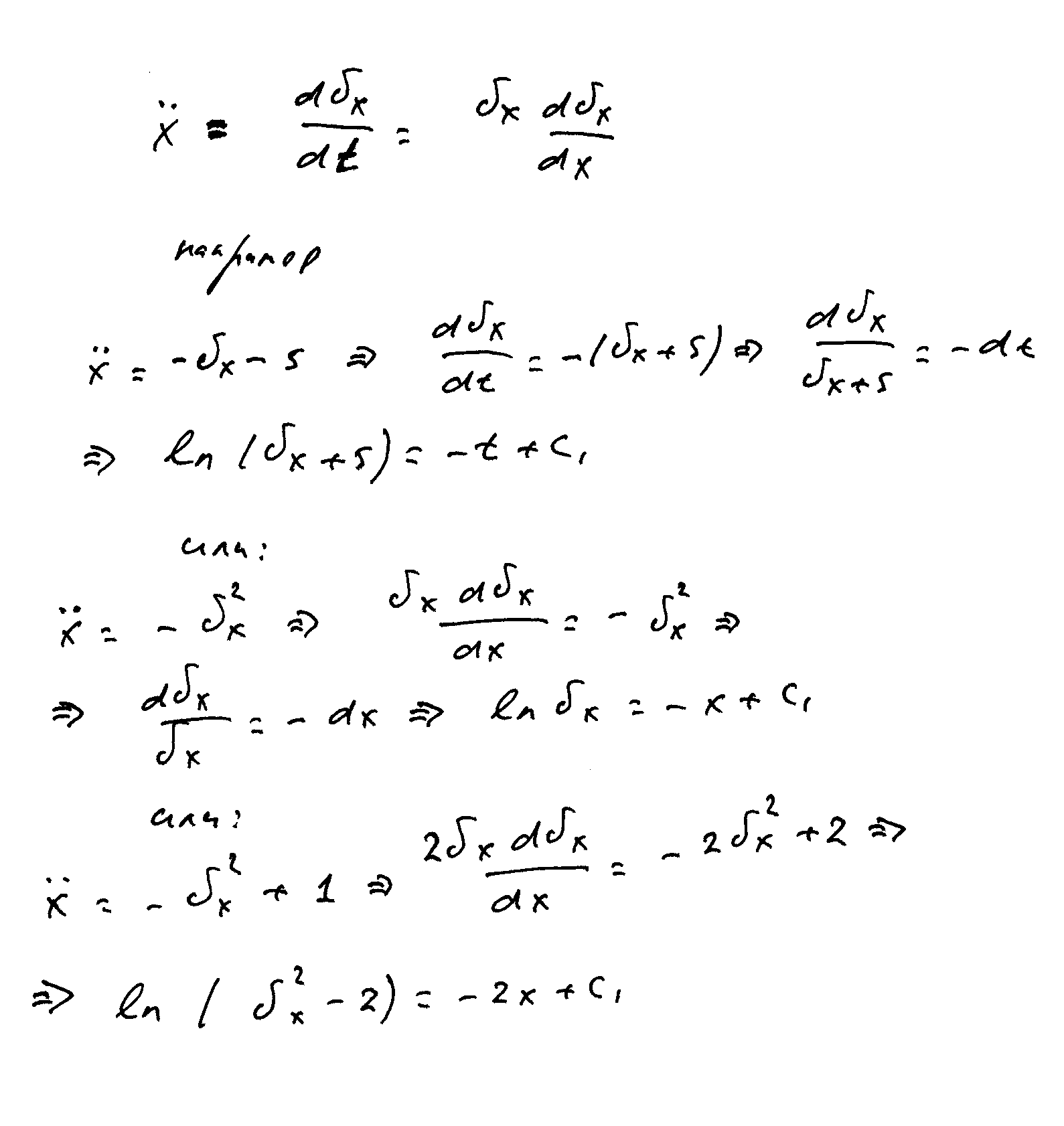 |
 Вход на сайт Вход на сайт
|



