Кинематический анализ плоского механизма Ищите кому заказать термех - пишите мне вк
Под кинематическим анализов в термехе как правило понимается кинематическое исследование (определение скоростей и ускорений характерных точек и звеньев механизма) плоского рычажного механизма или какой то системы колес соединенных между собой с помощью внутреннего или внешнего зацепления – такие системы как правило имеют водила и сателлиты (дифференциальные механизмы).
При всем своем многообразии (для ознакомления советую скачать у меня 30 задач К3 из Яблонского) решение сводиться к составлению векторных уравнений относительного движения, которые проецируются на оси координат. Соответственно предварительно вводится система координат. Из полученных уравнений находятся неизвестные величины. В одном векторном уравнении может быть не больше двух неизвестных, таким образом после проецирования на две оси координат получаются 2 уравнения и данная система может быть решена. Под неизвестными понимается величина или направление какого либо вектора. Уравнения могут иметь различный вид, но смысл примерно таков – что бы найти абсолютную скорость человека идущего по движущемуся автобусу требуется сложить векторы этих скоростей (скорости автобуса и человека относительно автобуса) . Так же и с ускорениями. Ниже я расписал физический смысл составляющих векторных уравнений; на рисунке а) показан кривошип – звено вращающиеся с угловым ускорением. Показаны формулы для определения скорости т.А и нормальных и тангенсальных составляющих ускорения т.А. Скорость точки перпендикулярна расстоянию между ней и осью вращения и направлена в сторону угловой скорости вращения “омега”. Нормальное ускорение – оно же центростремительное, направленно вдоль расстояния от точки до оси вращения и к этому центру. Касательное ускорение – перпендикулярно расстоянию до оси и в сторону направления углового ускорения – “эпсилон”. Расчетные формулы, для определения величин скорости и ускорения, написаны на рисунке.
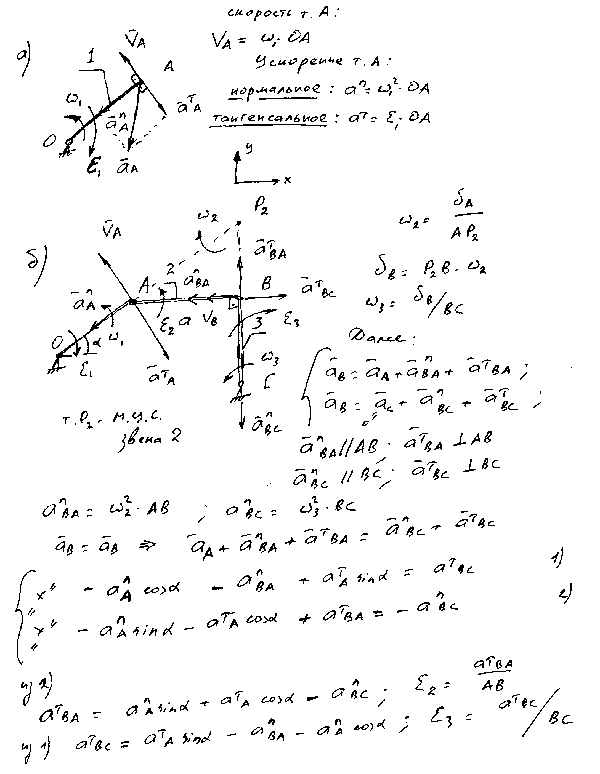 На рисунке б) нарисован весь механизм – в данном случае, как его называют, двухповодковый. Показано определение скоростей точек и звеньев этого механизма: расчет начинается с определения мгновенного центра скоростей звена 2 – точки Р2. Для этого проводятся перпендикуляры к скоростям двух точек принадлежащих рассматриваемому звену. Итак известно направление скорости точки А, так же очевидно, что скорость т.В направлена перпендикулярно ВС – получается, что нужно продлить линиями отрезки ОА и ВС, пересечение этих линий даст МЦС – мгновенный центр скоростей звена АВ (МЦС – это точка звена, которая в данный момент неподвижна. Далее определяется угловая скорость этого звена – как отношения скорости точки на расстояние от этой точки до МЦС. Далее определяется направление этой угловой скорости – если мысленно зажать пальцем МЦС и другим пальцем подпнуть т.А в сторону ее скорости то направление угловой скорости звена станет очевидным. Далее находиться величина и направление скорости т.В. Если бы на звене АВ была еще какая нибудь точка – ее скорость была бы найдена подобным способом. Далее составляются векторные уравнения для определения ускорения т.В ( как раз то, о чем я писал в самом начале). Так как движение т.В можно рассматривать как относительно т.А и т.С (двух автобусов) то и составим два векторных уравнения. Направление относительных нормальных ускорений определяем так: мысленно зажмем т.А и заставим звено 2 вращаться вокруг нее - очевидно что нормальное ускорение т.В относительно т.А будет направленно вдоль звена к т.А. Её численное значение определим по стандартной формуле – угловая скорость в квадрате умноженное на расстояние от т.В до оси вращения – в данном случае т.А. Нормальное ускорение т.В относительно т.С будет направленно вниз – к центру вращения звена 3. Касательные ускорения будут направлены перпендикулярно соответствующим нормальным – в какую именно сторону пока не известно, поэтому направление задается произвольно, если оно выбрано ошибочно, то его значение в результате расчетов будет отрицательным. Далее два уравнения приравниваются друг другу (так как очевидно, что ускорение т.В равно само себе), вводятся координатные оси, и векторное тождество проецируется на них. Из полученных уравнений находиться тангенсальные ускорения, зная которые легко определить полное ускорение т.В и угловые ускорения звеньев. В случае, если необходимо провести кинематическое исследование кривошипно-ползунного механизма, достаточно одного векторного уравнения и утверждения, что ползун двигается вдоль своей направляющей. Более подробно с примерами решений подобных задач вы можете ознакомиться бесплатно скачав с моего сайта 30 готовых задач из Яблонского семейства К3 и К4, причем в задаче К4 в более сложной форме дается решение подобных задач графическим методом – с применением плана скоростей и плана ускорений.
|
 Вход на сайт Вход на сайт
|



