Определение траектории движения точки , её скорости и ускорения по заданным параметрическим уравнениям движения

 Ищите кому заказать термех - пишите мне вк

 

 

 

Уравнение в координатной форме получается удалением параметра t – времени из параметрических уравнений движения. Для этого из одного уравнения выражается t и подставляется в другое. Либо, если функции тригонометрические, упрощаются с помощью применения стандартных, как правило простейших, тригонометрических преобразований (для того что бы функции были одного угла) и приводятся к уравнению окружности , эллипса, параболы или гиперболы (иногда даже прямой). 30 примеров из сборника задач по теоретической механике под ред. Яблонского из семейства К1 вы можете скачать бесплатно с моего сайта и более подробно рассмотреть возможные варианты приведения уравнений к координатному виду. 

 Ниже выкладываю свою заготовку - всё решение типовое. Необходим только минимальный навык в математике. 

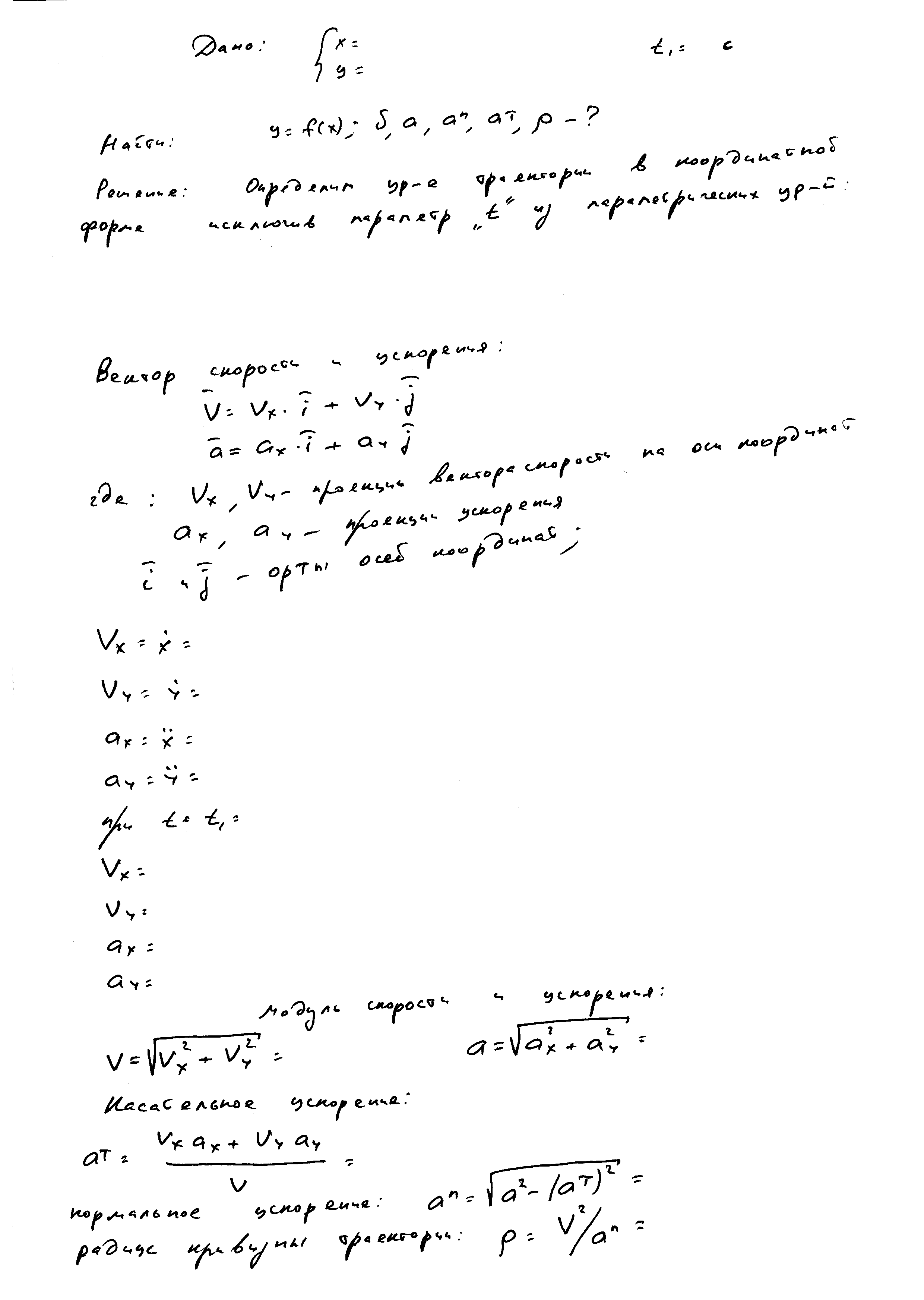 Вектора скорости и ускорения определяются составляющими – проекциями вектором скорости и ускорения на координатные оси. Эти проекции находятся путем дифференцирования параметрических уравнений движения по времени. Первая производная – скорость, вторая – ускорение. В полученные уравнения подставляться требуемое время – находятся проекции скорости и ускорения для необходимого моментв времени. Модуль скорости и ускорения находиться как векторная сумма проекций – те просто по теореме Пифагора, как корень от суммы квадратов проекций.  Далее определяется значение касательного (или как еще называют тангенсального) , нормального ускорений и радиуса кривизны траектории по стандартным для всех случаев формулам:

 

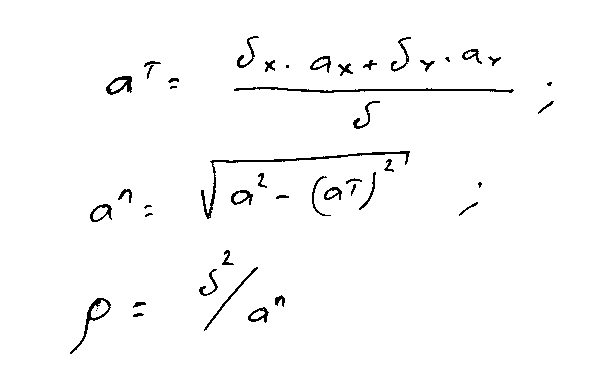 Далее находим координаты точки в начальный t=0, заданный и еще один моменты времени (еще один – это обычно заданный + 1 сек) по этим трем точкам строим в масштабе часть траектории движения. Показываем на ней точки положения в начальный момент и текущий,  для точки соответствующей заданному положению вычерчиваем в произвольно принятом масштабе проекции скорости – по их векторной сумме строим вектор скорости (он должен будет получиться направленным по касательной к траектории движения – это проверка номер 1 всего решения) . Соответственно показываться касательная и нормаль к траектории. Далее , опять таки в произвольно выбранном масштабе, вычерчиваются проекции ускорения, по их векторной сумме показываем вектор ускорения, проецируем этот вектор на нормаль и касательную – получаем на рисунке нормальное и касательное ускорения соответственно. Полученный ускорения должны совпадать по значению с ранее полученными численными значениями (это вторая проверка).