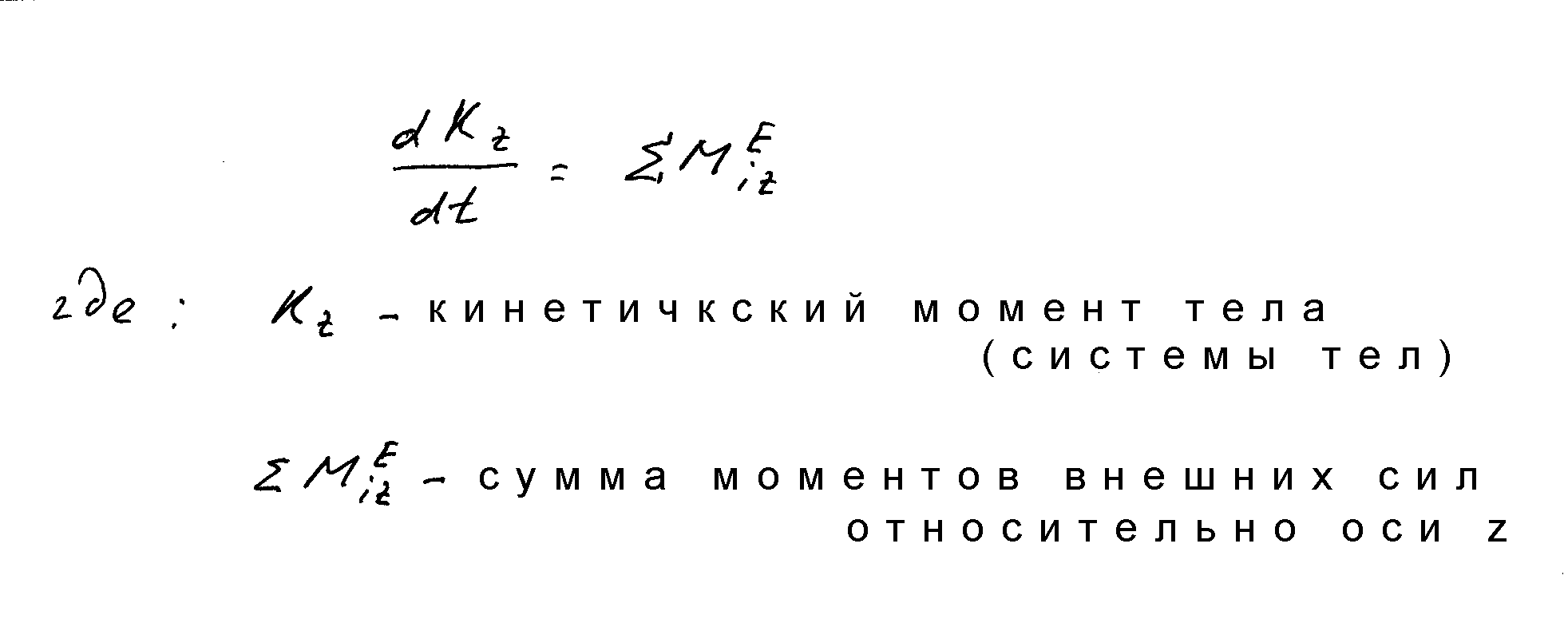
Теорема об изменении кинетического момента

 

 Кинетический момент системы относительно оси z  находим как сумму кинетических моментов всех её тел. Для тел, совершающих  вращательное движение кинетический момент равен произведению момента инерции тела относительно оси вращения на угловую скорость этого тела. Для материальной точки, совершающей движение по вращающемуся телу, кинетический момент находиться как сумма кинетического момента соответствующего относительному движению и кинетическому моменту соответствующему переносному движению. Каждый из них равен произведению массы материальной точки на скорость этого движения и на расстояние между осью вращения и линией проходящей вдоль вектора соответствующей скорости. Именно поэтому так называется теорема: нахождение  кинетического момента очень похоже на момент сил из статики, с той разницей, что тут он находиться не от силы, а от импульса mv . На этом этапе решения рекомендую не вставлять в выражения известные численные данные, по крайней мере хотя бы скорости.

 

 Сумма моментов внешних сил относительно оси вращения находиться как сумма моментов и произведений величин приложенных сил на расстояние между их линий действия и осью вращения. Стоит заметить два момента. Первое: что положительное направление кинетического момента и момента внешних сил совпадает, как правило это направление против движения часовой стрелки, но я рекомендую задаваться положительным направлением в сторону вращения тела в начальный момент времени. Второе: относительное движение очень часто задано в виде закона зависящего от времени, в этом случае следует в выражение для подсчета кинетического момента соответствующего относительному движению подставить зависимость этой скорости от времени. 

 

 После того, как получены выражения для определения кинетического момента системы и суммы моментов внешних сил начинается высшая математика – дальнейший ход решения зависит от начальных данных и от того какую величину по заданию требуется найти. 

На ум приходят два сценария дальнейшего решения: можно разделить переменные и проинтегрировать обе части тождества, правую по угловой скорости, а левую по времени, с пределами интегрирования соответствующими параметрам начала движения и конечного (текущего) момента времени. Или можно найти неопределенный интеграл от сумы моментов сил по времени и приравнять его к выражению для определения кинетического момента. Для определения постоянной интегрирования ввезти в тождество начальные условия. Ну а дальше останется только найти из полученного выражения искомую величину.  В качестве примера задач на эту тему можно скачать у меня с сайта задачи  из Яблонского из семейства  Д9 и из Мещерского параграф 37.