Сложное движение точки – термех кинематика. относительное и переносное движения- определение абсолютной скорости и ускорения точки.

 

 

Примеры моих решений:   Пример1   Пример2

 

 Задачи по теоретической механике на  сложное движение точки довольно часто задаю для решения студентам, поэтому я решил вкратце объяснить как решать типовые задачи на эту тему.  Суть задачи сводиться такова – что то движется по чему то вращающемуся, например человек идет по земле (иногда наоборот – что то вращается на чем то поступательно движущемуся, например пропеллер на самолете, но такие случаи встречаются крайне редко), задан закон относительного и переносного движений. Требуется определить абсолютную скорость и абсолютное ускорение точки в заданный момент времени. Алгоритм движения стандартен абсолютно во всех задачах этого типа. Введем определения: относительным движением назовем движение точки по движущемуся телу (движение человека по Земле). Переносным движением – движение точки вместе с телом относительно неподвижной, стационарной системы координат (вращение точки относительно оси вращения Земли).

 

 Решение задачи начинается с рассмотрения относительного движения, оно обычно обозначается индексом “r” (смотри пример).Дифференцируя закон относительного движения (как правило он задан в естественном виде)  и подставляя в полученные уравнения заданный момент времени  получим скорость относительно движения – первая производная, касательное ускорение – вторая производная, и нормальное ускорение – как отношение квадрата скорости к радиусу кривизны относительного движения. Если относительное движение совершается по прямой, то нормально ускорения не будет (так как радиус кривизны в этом случае равен бесконечности). Далее подставляем заданное время в закон движения и определяем положение точки на рисунке в данный момент, показываем векторы всех найденных выше величин. Заметим, что относительная скорость и относительно касательное ускорение всегда направлены по касательной к траектории, по которой точка движется по вращающемуся телу. Нормальное относительное ускорение всегда направленно к центру относительного движения (по нормали к касательной – перпендикулярно скорости к центру вращения). После всего этого следует определить расстояние от точки до оси вращения тела (назовем это расстояние ММ’). Делается это с помощью простых геометрических расчетов. 

 

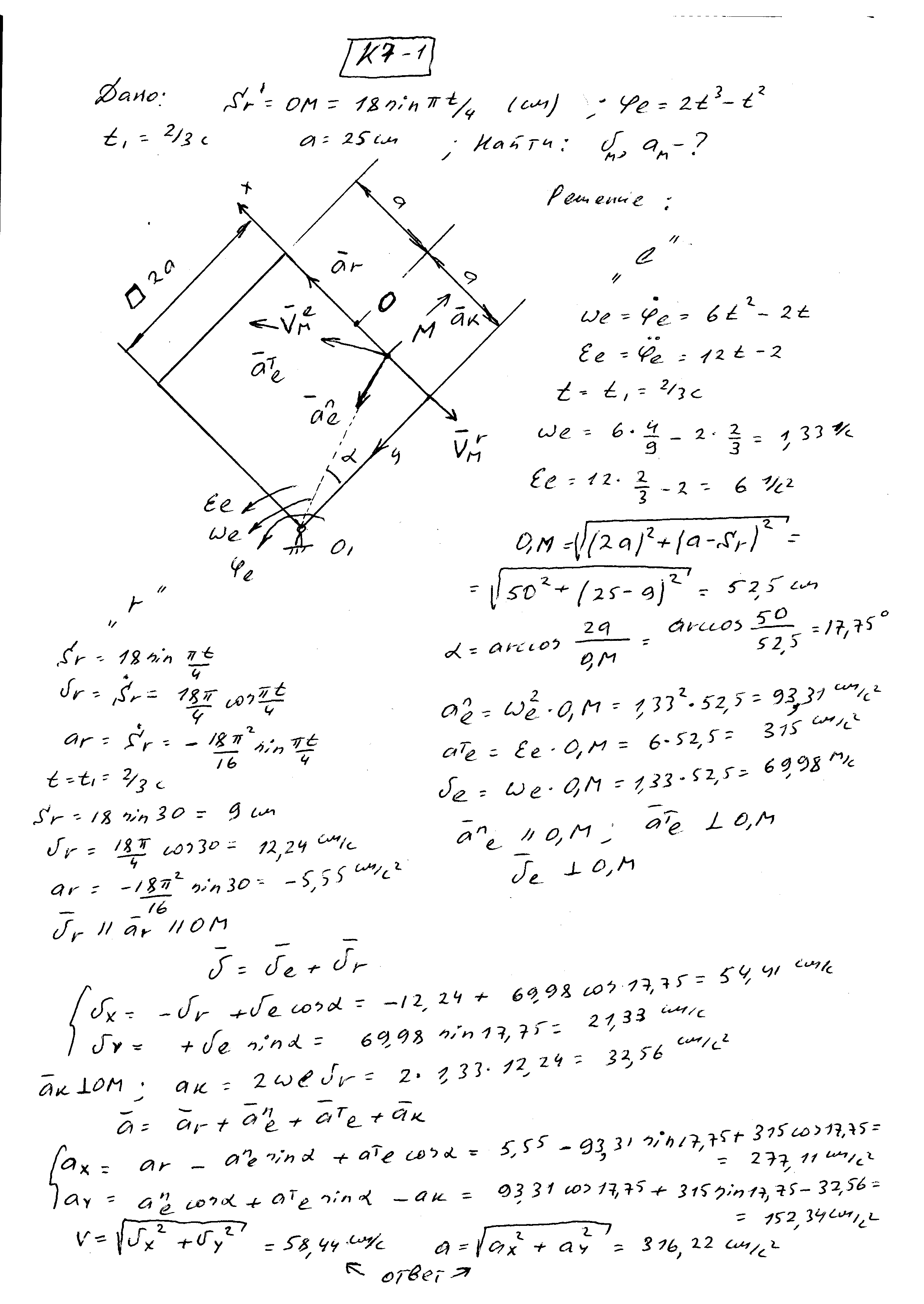Далее рассматривается переносное движение точки, которое обозначается индексом “l” . Зная закон вращения тела вокруг своей оси, находим выражения для угловой скорости – первая производная, углового ускорения – вторая производная. Подставляем заданное время – находим численные значения угловой скорости и углового ускорения переносного движения. Далее определяем значение переносной скорости – это произведение расстояния от точки до оси вращения (ММ’ – ранее найденное) на значение угловой скорости переносного движения. Скорость направлена перпендикулярно этому расстоянию в сторону вращения тела. Далее находим касательное – ММ’ умноженное на угловое ускорение (направленно перпендикулярно  ММ’ в сторону углового ускорения), и нормальное  ускорение – угловая скорость в квадрате умноженная на расстояние ММ’ (направленно параллельно ММ’ к оси вращения тела).  В редких случаях, когда переносное движение не является вращательным, а поступательным – то просто дифференцируют дважды заданный закон переносного движения, подставляют время и показывают на рисунке направление векторов, в этом случае ускорения Карриолиса не будет иметь места вообще. 

 

Далее определяется ускорение Кориолиса, численно оно равно удвоенному произведению переносной угловой скорости на велечину относительной скорости помноженной на косинус угла между плоскостью перпендикулярной оси вращения тела и вектором относительной скорости. Направление ускорения Кориолиса определяется по следующему правилу: что бы определить направлениу ускорения Кориолиса, необходимо спроецировать вектор относительной скорости на плоскость перпендикулярную оси вращения тела и повернуть полученную проекцию на 90 градусов в сторону вращения переносной угловой скорости.  

 

Далее все просто – чтобы определить значение абсолютной скорости и ускорения необходимо векторно сложить все полученный величины ( те веткор абсолютной скорости это сумма вектром относительной и переносной скоростей, вектор абсолютного ускорения – это сумма векторов относительного нормального и касательного ускорения с переносными нормальным и касательным ускорениями и ускорением Кориолиса.). Далее вводяться координатные оси, векторные ускорения на них проецируються, в полученные уравнения подставляються ранее найденные величины. По теореме Пифагора определяем модули значений абсолютной скорости и ускорения . The End