Решение задач на применение уравнений Лагранжа второго рода Ищите кому заказать термех на Лагранжа 2 рода? - пишите мне вк!
На этой теме я позволю себе закончить описание решения типовых задач по теоретической механике. Задачи на применение уравнения (или уравнений – если система имеет несколько степеней свободы) Лагранжа – одни из самых сложных в курсе теоретической механики. Поэтому они редко выдаются преподавателям для самостоятельного выполнения. Но иногда такое все таки случается. В сборнике задач для индивидуального выполнения по теоретической механике под редакцией проф. Яблонского А.А. есть две задачи на эту тему которые я полностью промешал (а это по 30 задач в каждой – в сумме 60). Это Д21 (система с двумя степенями свободы) и Д23 (на колебание системы с одной степенью свободы). Все эти задачи, перейдя по ссылкам, вы можете скачать абсолютно бесплатно . Так же на Лагранжа второго рода есть целый параграф (48 – можно скачать бесплатно у меня) в Мещерском, который я тоже прорешал.
Итак – методика решения задач по термеху на Лагранжа. Сперва перерисовываем схему, показываем на ней все внешние и внутренние силы (из внутренних стоит показать силы, с которыми действуют друг на друга тела входящие в состав системы – реакции опор, силы упругости и трения). Потом задаемся обобщенной координатой (если система имеет несколько степеней свободы – то соответственное число обобщенных координат) и показываем ее на рисунке. Далее следует записать уравнения Лагранжа второго рода в общем виде, число уравнений равно числу степеней свободы механизма:
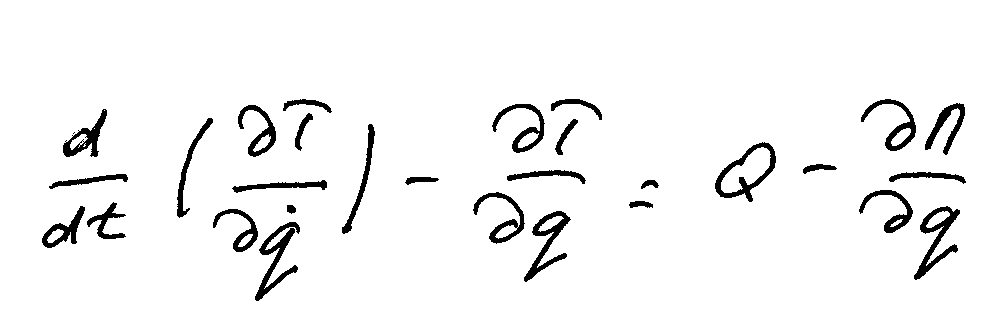 Тут : Т – кинетическая энергия системы, сумма кинетических энергий все тел, выраженная через первую обобщенную координату.
q – обобщенная координата. Обычно, если движение у тела поступательное – обобщенную координату обозначают как икс, а если вращательное – как фи.
Q – обобщенная сила.
П – потенциальная энергия системы.
Далее находиться кинематические характеристики между изменением обобщенной координаты (координат – если несколько степеней свободы) и скоростями центров масс и угловых скоростей остальных тел системы. Если проще – скорости всех тел выражаються через обобщенную координату. Если число степеней свободы несколько, то обязательно скорость какого то хотя бы одного тела будет зависеть от нескольких обобщенных координат. Кинематические соотношения находятся так же как в задаче К2 или Д10 из Яблонского, из условия неразрывности связей и движения колёс без проскальзывания.
Далее найдем обобщенную силу, или потенциальную энергию или и то и другое. Логика такая – если по заданию требуется определить статическую деформацию пружины (те пружина в задаче есть) то без потенциальной энергии не обойтись, если этого не требуется - то можно обойтись нахождением обобщенной силы. Если уж надо находить потенциальную энергию, то обобщенную силу находить не будем, так как мы лодыри)
Итак, обобщенная сила ищется так:
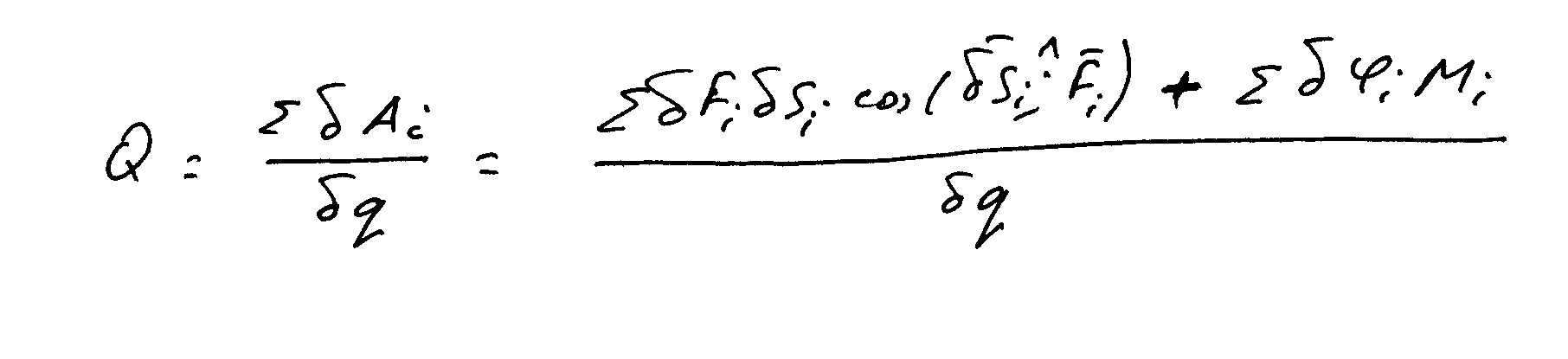 те сумма бесконечно малых работ на бесконечно малом перемещении принятой обобщенной координаты делим на само бмв перемещение о.координаты. Причем если обобщенных координат две, то другую обобщенную координату как бы мысленно останавливаем, те ее бмв перемещение пусть будет равно нулю. В свою очередь, когда будем находить выражение для обобщенной силы для уравнения в котором фигурирует другая обобщенная координата не будем учитывать изменение первой о.координаты. Более подробно нахождение обобщенных координат для систем с двумя степенями подвижности рекомендую рассмотреть на примерах моих задач Д21 из Яблонского. Потенциальная же энергия будет находиться как сумма двух потенциальных энергий системы: потенциальной энергии тел в гравитационном поле и от воздействия других внешних сил: активных сил, моментов и сил трения между телами системы и потенциальной энергии пружины. Более подробно ход решения подобных задач хорошо виден на примерах решения задач Д23 из Яблонского. После того, как выражение для нахождения потенциальной энергии (или обобщенной силы) найдено приступаем к составлению уравнения (уравнений) Лагранжа второго рода.
Тут все достаточно просто: необходимо найти частные производные кинетической энергии а) по каждой из обобщенных координат (как правило они равны нулю, но иногда бывают исключения) б) по скорости изменения каждой из координат, а потом и по времени. Далее находим частную производную потенциальной энергии по обобщенной координате.
Ну вот пожалуй и все, далее из полученных выражений составляется уравнение (уравнения) Лагранжа второго рода, по сути оно получиться дифференциальным уравнение м второго (иногда со специальной правой частью). С учетом данных начальных условий решаем это уравнение, находим все искомые величины.
|
 Вход на сайт Вход на сайт
|



